Imagine you’re the star of an action movie about a kidnapping. As part of the story, you come into possession of a secret message, which says where the victim is hidden. Unfortunately, the message is encrypted using a 12-digit secret key, i.e., a string of digits such as . But you don’t know the secret key. The only way to unlock the message and find the victim is by searching through the (one trillion) possible keys. While you may get lucky and find the right key early on, on average you’ll need to try different keys, and in the worst case you’ll need to try all .
I’ve painted a fanciful picture, but similar search-based algorithms are used frequently in computing. They’re often the first approach we try when solving a problem. For example, suppose you’re trying to attack the famous traveling salesperson problem (TSP), that is, trying to find the shortest route that visits every city in a list of cities, while returning to the origin city. A simple approach is to search through all the possible routes, while keeping track of the minimal route found. Of course, it’s possible to develop more sophisticated algorithms for TSP, algorithms that make it unnecessary to search through every route. But that doesn’t take away from the core point: for many problems in computing a search-based approach is a good first-cut way to attack the problem. Indeed, search is sometimes a good final-cut approach, or even provably optimal. Overall, search is an exceptionally useful general-purpose algorithm.
As mentioned above, on a conventional classical computer, if we have a search space of items, we need to examine the search space on the order of times to find the item we’re looking for. Remarkably, quantum computers can do far better. It turns out that you can use a quantum computer to solve the search problem after examining the search space roughly times! A little more precisely, it needs to examine the search space about times. That square root factor makes a big difference. If was a trillion, as in our opening scenario, then a classical computer will need to examine the search space a trillion times, while the quantum computer will need to examine it fewer than 800 thousand times. That’s an improvement of more than a factor of a million.
When I first heard about the quantum search algorithm I thought it sounded impossible. I just couldn’t imagine any way it could be true. But it is true. In this essay I explain in detail how the quantum search algorithm works. I’ll also explain some limitations of the quantum search algorithm, and discuss what we can learn about quantum computing in general from the quantum search algorithm.
To read this essay you need to be familiar with the quantum circuit model of computation. If you’re not, you can learn the elements from the earlier essay Quantum Computing for the Very Curious.
It may be tempting to think “Oh, I'm not that interested in the problem of search, why should I bother learning about it?” But the point of this essay is deeper than search. It's to begin answering the question: how can we use quantum computers to do things which are genuinely different and better than a conventional classical computer? The particular problem (search) is almost incidental. And so the essay is about learning to think in the quantum realm, finding non-classical heuristics that let us beat classical computers. This turns out to be immensely challenging, but also immensely fun.
Because of these aspirations, I won’t just explain how the search algorithm works. We'll dig down and try to understand why it works, and how you might have discovered the algorithm in the first place. That takes more time than just laying out the quantum circuit, but is also more rewarding. Along the way we’ll learn many other techniques widely used in quantum algorithm design, ideas such as clean computation, the phase trick, quantum parallelism, and others. All this is great experience in learning how to think about quantum algorithm design in general.
This essay is an example of what Andy Matuschak and I have dubbed a mnemonic medium – it’s like a regular essay, but incorporates new user interface elements intended to make it almost effortless for you to remember the content of the essay. The motivator is that most people (myself included) quickly forget much of what we read in books and articles. But cognitive scientists studying human memory have understood how to guarantee you will remember something permanently. This mnemonic medium builds those ideas into the essay, making it easy to remember the material for the long term.
The core idea of the mnemonic medium is this: throughout the essay we occasionally pause to ask you a few simple questions, testing you on the material just explained. In the weeks ahead we’ll re-test you in followup review sessions. By carefully expanding the testing schedule, we can ensure you consolidate the answers into your long-term memory, while minimizing the study time required. The review sessions take no more than a few minutes per session, and we’ll notify you when you need to review. The benefit is that instead of remembering how the quantum search algorithm works for a few hours or days, you’ll remember for years; it’ll become a much more deeply internalized part of your thinking.
Of course, you can just read this as a conventional essay. But I hope you’ll at least try out the mnemonic medium. To do so please sign up below. This will enable us to track the best review schedule for each question, and to remind you to sign in for occasional short review sessions. And if you’d like to learn more about how the mnemonic medium works, please see A medium which makes memory a choice, How to approach this essay?, and How to use (or not use!) the questions.
As an example, let’s take a look at a couple of simple questions reviewing what you’ve just learned. Please indulge me by answering the questions just below. It’ll only take a few seconds – for both questions, think about what you believe the answer to be, click to reveal the actual answer, and then mark whether you remembered or not. If you can recall, that’s great. If not, that’s also fine, just mentally note the correct answer, and continue. Since you probably weren't expecting to be tested like this, it seems only fair to give you a hint for the second question: the somewhat hard-to-remember prefactor in the answer is . Later in the essay I won't always provide such reminders, so you'll need to be paying attention!
The building blocks of the quantum search algorithm
In the introduction I gave an informal description of what the quantum search algorithm achieves. To make the search algorithm more concrete, let’s think about the special case of using search to attack the traveling salesperson problem (TSP). Of course, there are better approaches to TSP than search, but the purpose of this section is to show the overall building blocks that go into the search algorithm. For that purpose, TSP is a useful concrete example. In the next section we’ll understand the details of how the buildings blocks work.
It’ll help to consider a variation on TSP, namely, searching for a route shorter than some specified threshold distance, . In other words, we’ll be using search to solve problems like:
Here’s a list of cities – Hobbiton, Minas Tirith, Edoras, Bree, Dale, … – and the distances between them (which I won’t attempt to specify, but you can imagine!) Is there a route through all the cities that is less than 2,000 kilometers [or the equivalent in miles] in length?
This isn’t quite the same as find-the-minimal-route, but this variation turns out to be a little easier to connect to the quantum search algorithm. Variation noted, here’s what a quantum search algorithm might look like:
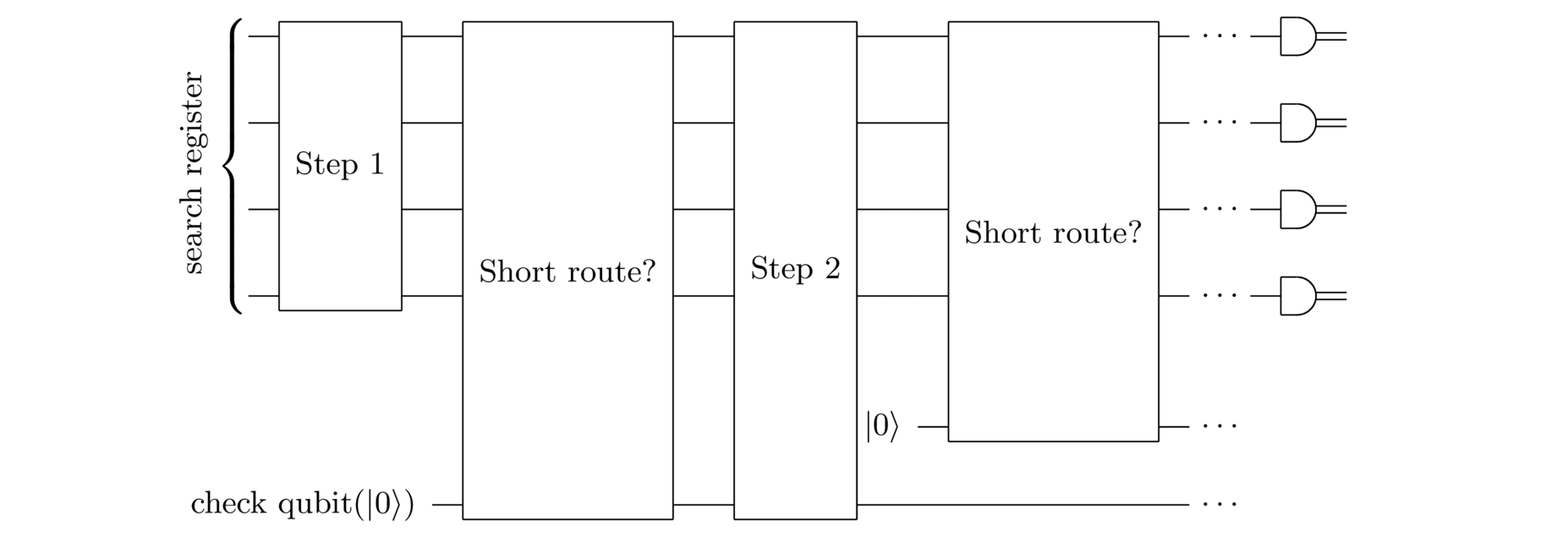
The search register contains candidate solutions to the search problem. In this case, our search register will contain potential routes through the cities, written out as bit strings . I won’t get into the bit string representation explicitly – there are many ways to make such a representation, and the details don’t much matter. The key point is that you should think of the search register as being in some superposition of different possible routes through the cities, and as being some bit string representation of a route.
For definiteness, I’ll also assume the search register starts in the all state. That’s just a convention: we need to start somewhere.
Step 1 of the quantum search algorithm will just be some fixed quantum circuit, made up of standard quantum gates – things like the Hadamard and CNOT gates, as discussed in the previous essay. Of course, eventually we need to figure out what those gates should be. We’ll do that in later sections. But for now we’re just sticking at a broad conceptual level, trying to figure out what a quantum search algorithm might look like.
The next step is to check if the search register state corresponds to what we’ll call a short route through the cities, i.e., a route of less distance than the threshold . To do this, we introduce a check qubit to store the results of this step, initialized in the state . So we start in the state , and change to if represents a short route through the cities, and otherwise are left as , when doesn’t represent a short route. We can write this compactly as , where the search function is equal to if is a solution to the problem (i.e., a route of length less than ), and if is not a solution.
Of course, in general the search register is in a superposition . We’ll assume (and justify later) that this checking-if-short-route step acts linearly, taking to .
How is this checking-if-short-route step implemented? Of course, in principle it’s easy to construct a conventional classical circuit which does the trick – the circuit would just check that the bit string is a valid route through all the cities, and if so would add up the corresponding distances, and compare it to the threshold . We can just take that classical circuit – whatever it is – and translate it into the equivalent quantum circuit. I explained how to do such translations using Toffoli and NOT gates in the earlier essay, and I won’t re-explain it here. Of course, we still need to figure out the exact details of the classical circuit, but: (a) that’s part of classical computing, not quantum computing; and (b) in any case is a detail unrelated to making search work. With one slight caveat (to be discussed shortly), we’ll take for granted we have a quantum circuit which can do the job.
After that is Step 2 in the quantum search algorithm. Again, we need to figure out exactly what quantum gates to use here, and we’ll do that in the next section.
Next, we check again if the search register state is a short route. It works just as before, with a check qubit and so on.
We continue in this way, alternating steps in our search algorithm with checking whether or not the search register state is a solution to our search problem, i.e., a short route through the cities. At the end of the algorithm we measure the search register. If we’ve designed the search algorithm well, then the result of the measurement will be a solution to the search problem, in this case a route through the cities of distance less than .
A challenge is that sometimes such a solution may not exist. In our example, that’ll happen when there is no route through the cities of distance less than . In that case, whatever measurement result we get at the end of the search algorithm, it won’t be a solution to the search problem. That’s okay, though, since it’s easy to just check and make sure we’ve got a legitimate solution.
I’ve been talking about the problem of searching for short routes in TSP. But there’s little here that has to do with the details of TSP. We can imagine a general quantum search algorithm which works along the same lines:
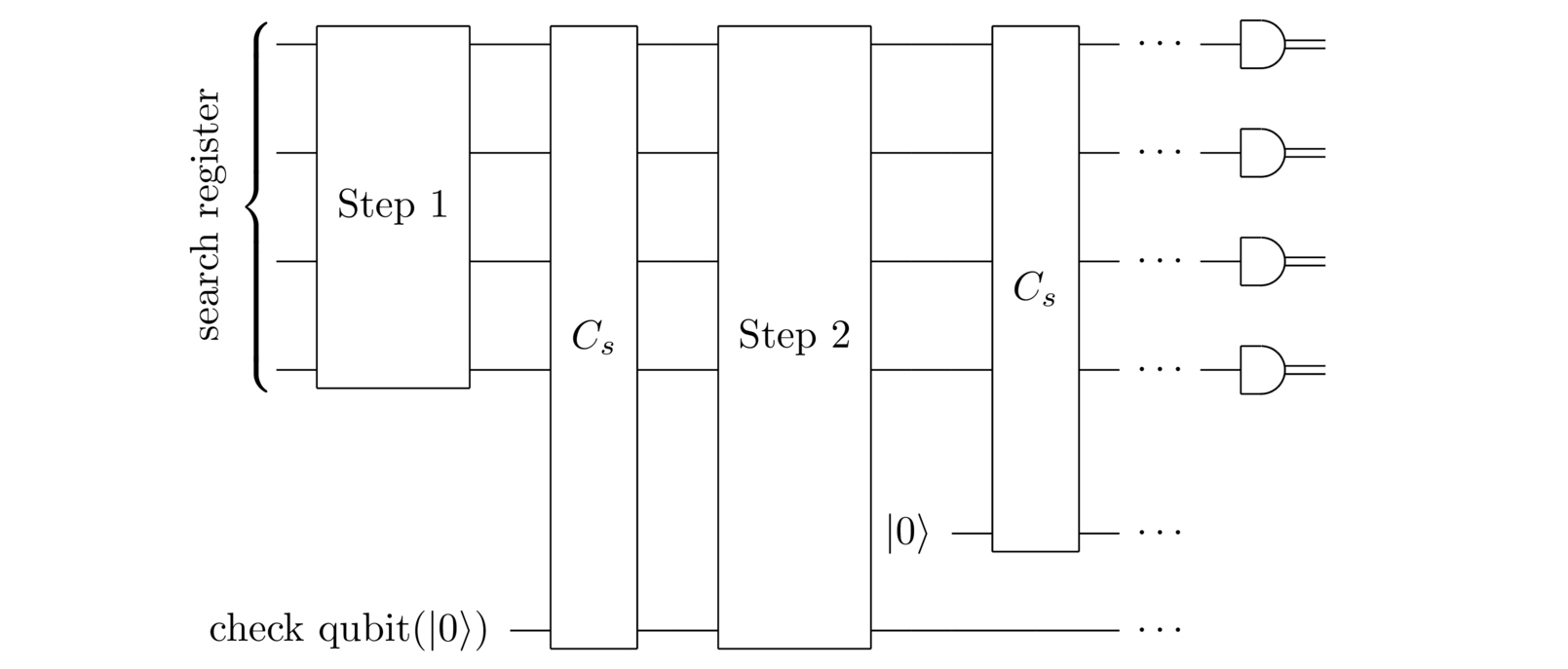
Everything is the same, except that we’ve replaced the check-if-short-route step by . We can think of this as a subroutine or black box which checks whether or not the search register is a solution to the search problem. In particular, we’ll assume that takes to , where (to recap) the search function when is not a solution to the search problem, and when is a solution to the search problem. More informally, we can think of as examining the search space to see if the search register contains a solution to the search problem. The hope motivating the quantum search algorithm is that we can reduce the number of times we need to do such examinations. In particular, we’ll try to minimize the number of times the search black box needs to be applied.
As another example, suppose the search problem is the one I opened the essay with – searching for a key to decode a kidnapper’s note. In that case, you’d design so it does two things: (1) decodes the kidnapper’s note, assuming the search register contains a possible key; and (2) examines the decoded text from step 1 to see whether or not it’s plausibly a message in English. If it is a plausibly an English message then almost certainly it’s the correct text, since for most ciphers decodings for anything other than the correct key will look like gibberish. All of this is easily done using classical circuits, and those classical circuits can then be converted into a suitable quantum circuit for .
As still another example, consider the protein folding problem – the problem of figuring out what shapes proteins take on in nature. A way of phrasing this in our framework is as a search for a way of spatially arranging the protein’s amino acids so the protein’s energy is below some threshold energy, ? If you can answer this question reliably, then by gradually lowering the threshold you can find the lowest-energy states for the protein. These lowest-energy states correspond to the shapes we find in nature. Again, it’s easy to figure out a circuit which checks whether or not some potential spatial arrangement of the amino acids has energy less than .
For the purpose of designing the quantum search algorithm we’re not going to worry about how the search black box works. We’ll just assume you’ve got access to a suitable . Indeed, much of the utility of the quantum search algorithm comes from the fact that it works with any . Of course, to actually implement the quantum search algorithm in practice we’d need to have an actual implementation of a suitable . But to design a useful quantum search algorithm, we can treat as a black box.
So our main job through the remainder of this essay is to figure out how to design the quantum circuits for step 1, step 2, and so on, in order to minimize the total number of times we need to apply the search black box. We’ll design those quantum circuits in the next section.
Incidentally, people new to the quantum search algorithms sometimes get a little hung up because of the slightly mysterious-sounding term “black box”. They worry that it implies there’s some sort of sleight-of-hand or magic going on, that quantum search must require some sort of genie wandering around giving out black boxes. Of course, it’s not magical at all. To repeat what I said above: if you were actually running the search algorithm, you’d need an implementation of the black box for your particular problem. But the point is to design a search algorithm which works no matter the internal details of the search black box – it abstracts those away.
Another common misconception is that to implement the search black box we would need to know the value of in advance. That’s not necessary because there’s a big difference between a circuit which can recognize a solution and which knows the solution. All the search black box needs is to be able to recognize a solution. For instance, it’s obviously possible to design a circuit which can recognize a short tour through a list of cities, without explicitly knowing a short tour in advance. Similarly for recognizing low-energy protein shapes, recognizing a decoded kidnapper’s note, and so on.
Having spent so much time saying that we’re not going to worry about the details of I’ll now turn around and say that it simplifies things a little if we make one extra assumption about the search black box: we’ll suppose there is exactly one solution to the search problem. This assumption is ultimately not essential – the search algorithm can be extended to the case of multiple (or zero) solutions. But for now it simplifies life to assume there’s exactly one single solution, which we’ll label . That, by the way, is why I labeled the black box .
(Incidentally, the search black box is sometimes called a search oracle, since it’s this oracular thing which tells us whether we have a solution to the search problem or not. I use the term black box in this essay, but many people use the term “oracle”, and it’s worth being aware of both terms.)
Getting a clean black box: Earlier, I blithely asserted you can take a classical circuit for computing the search function , and turn it into a quantum circuit which has the effect .
Actually, there’s a slight complication. To illustrate the issue concretely, suppose you’re trying to compute , that is, the AND of three bits (corresponding to a search solution , in binary). To do this, we’d start by using a Toffoli gate to compute the AND of the first two bits, :
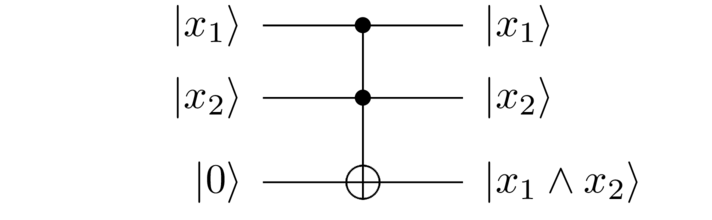
Then we’d use another Toffoli gate to AND the result with :
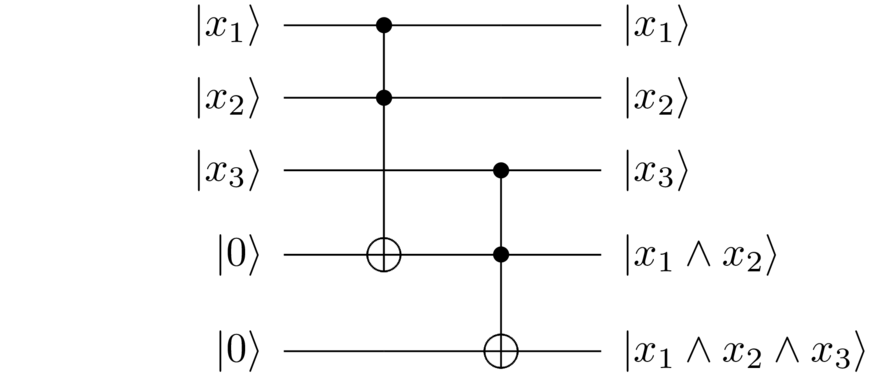
So we’ve indeed computed , but along the way we’ve also generated an intermediate working qubit in the state . That working state wasn’t part of our original specification. Put another way, we wanted to compute
and instead we ended up computing
More generally, suppose we try to convert a classical circuit computing the search function into a quantum circuit. If we do it using the recipe described in the last essay – converting AND gates to Toffoli gates, and classical NOT gates to quantum NOT gates – it won’t take to . There will be extra qubits involved, arising as intermediaries during the computation. The result will be something more like
where the extra register is a supply of one-or-more working qubits, and they end up in some state produced along the way.
The difference might seem small. We’re certainly close to having our search black box. But it turns out to be crucial to the quantum search algorithm that we get that clean behavior, . We’ll discuss later why this clean form for the computation is needed. For right now, though, let’s figure out how to do it.
Fortunately, there’s a simple trick called uncomputation which works. It involves three steps. The first is more or less what you’d expect, but the second and third are quite clever:
- Compute , using the standard approach of converting classical AND gates to Toffoli gates, and classical NOT gates to quantum NOT gates.
- Add on an extra qubit in the state, and do a CNOT with as the control. This effectively copies the result, and we obtain: .
- Now apply all the gates from step 1, but in reverse order, and applying at each step the inverse gate. The result is to undo or uncompute what happened in step 1, resulting in .
At the end, we can ignore the state, which isn’t changed at all by the entire process. And so the net result of these steps is the desired transformation, .
Summing up, if we have a classical circuit to compute a function , you can think of the three stages in the corresponding clean quantum circuit as: compute , by converting classical gates to quantum; copy the answer using a CNOT; uncompute, by reversing the gates and inverting them.
So, for instance, it’s easy to convert a computation of into the clean form using uncomputation. We just literally follow the steps above, and remember that the inverse of a Toffoli gate is a Toffoli gate:
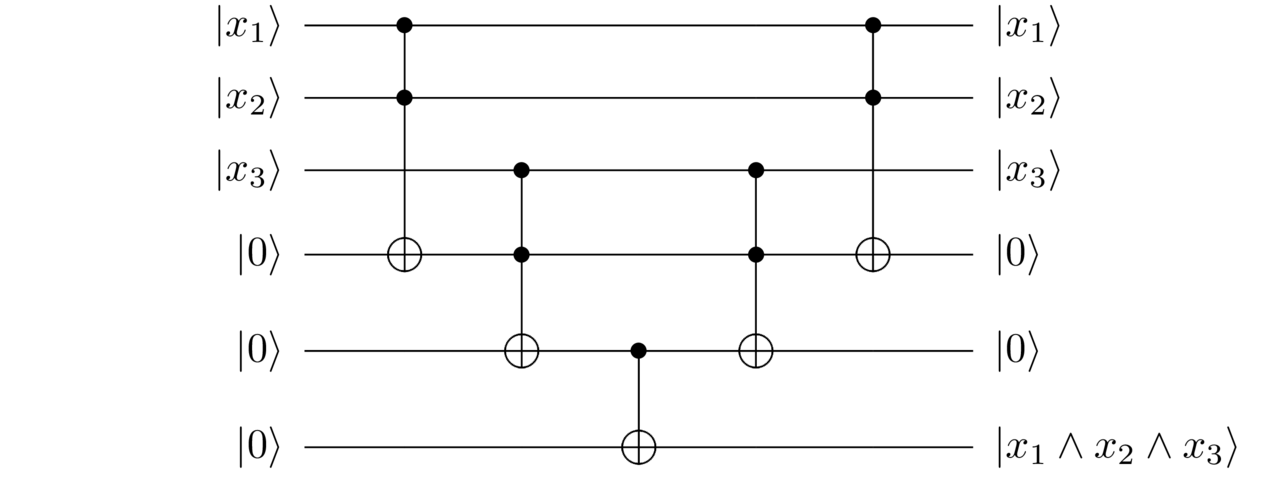
I’ve written the results of the clean computation as . What would have happened if the second register had been in the state (or, more generally, an unknown state or ), instead of ? You can easily trace through the above steps to see that the net result is
where the addition is done modulo . This type of clean computation turns out to be useful in many quantum computations, not just quantum search, and the form just shown is the standard form in which it is presented. In particular, we can do a clean computation of any function for which we have a classical circuit, not just search functions. In any case, we will assume that the form given in the equation just above is the effect of the search black box .
It’s worth noting that there is a price to pay in converting a classical circuit to its equivalent clean form: the uncomputation step doubles the number of gates required, and the copying step adds an extra CNOT on top of that doubling. So there is a genuine overhead in getting to the clean form. Still, for the speedup we’ll get from the quantum search algorithm this is a tiny price to pay.
Exercise: Find a quantum circuit which computes , where denotes the logical OR.
Exercise: Find a quantum circuit which performs a clean computation of the classical function .
Let me finish the discussion of clean computation by introducing some extra pieces of quantum circuit notation that will come in handy later. The notation I’ll introduce generalizes the CNOT and Toffoli gates to involve more control qubits. For instance, here’s an example involving three control qubits:
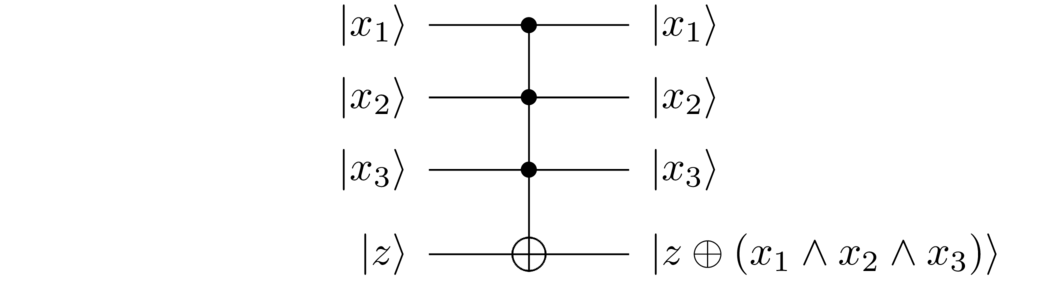
It behaves as you’d expect, NOTting the target qubit when all three control qubits are set, and otherwise leaving it alone. We just saw how to implement this using Toffoli gates and uncomputation:
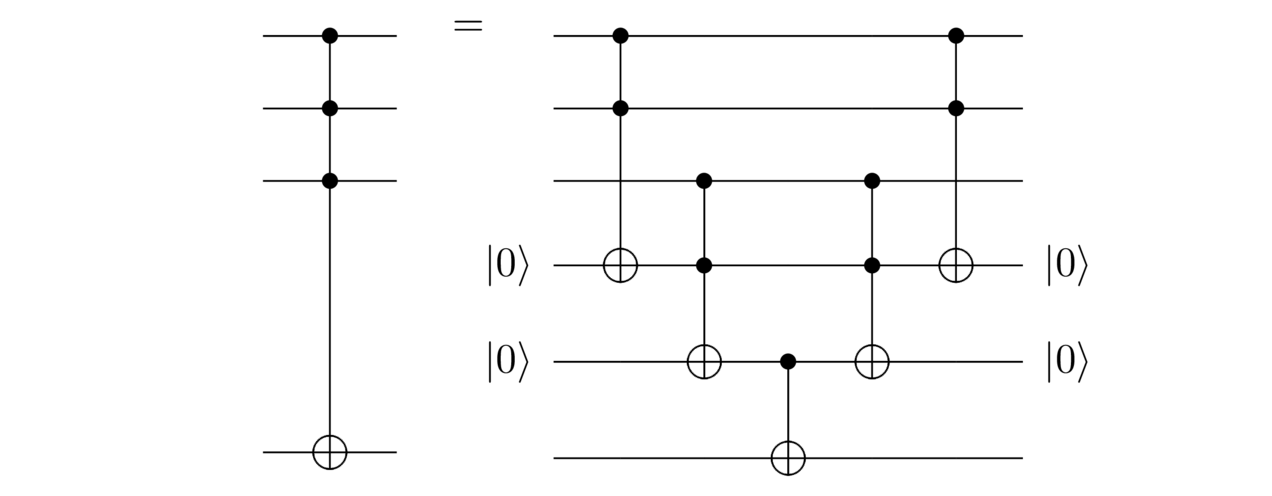
If we want to break this down even further, we can use techniques from the last essay to break the Toffoli gates into one- and two-qubit quantum gates.
Very similar ideas can be used to synthesize even more complicated controlled gates, e.g. gates controlled by four qubits such as:
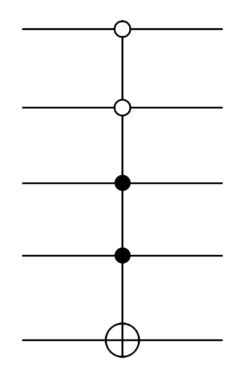
In this notation, an open circle on a control qubit means gates are applied conditional on those control qubits being set to . In this case, it means the NOT on the target qubit is applied conditional on the first two qubits being set to and the third and fourth being set to . I’ll leave it to you to figure out the details of how to break this down into Toffoli and other standard quantum gates – it’s a good exercise in applying the ideas we’ve been learning.
Exercise: Find a way of breaking the controlled gate shown just above (with four control qubits) down into Toffoli and one- and two-qubit quantum gates.
Database search? The quantum search algorithm is sometimes described as a database search algorithm. This is often done in popular media accounts, and sometimes even in research papers. Unfortunately, it’s not a terribly helpful way of thinking about it. For one thing, databases are usually ordered, and that ordering makes them extremely fast to search. For instance, suppose you have an alphabetically ordered list of surnames:
Calder
Davies
Jones
Ng
Prothero
Richards
…
To find out if a name is on the list you wouldn’t run through the entire list. Rather, you’d exploit the ordering to do some kind of binary search. The result is that instead of needing to examine the database times, you only need to examine it on the order of times. That’s vastly faster than the order times required by the quantum search algorithm. If someone needs to examine a database times in order to search it, it probably means they need to think harder about how they’re indexing their database.
Why is the notion of a quantum database search used so often in explanations? My guess is that it’s because searching a database is the most obvious really concrete way of thinking about search. But it’s that very concreteness which makes it easy to build database indices, which usually make database search a trivial problem in practice. Search is vastly more challenging when it’s hard to find or exploit any structure in the search space, in problems like decoding a code or the TSP or protein folding. It’s in such cases that the quantum search algorithm will shine. More precisely: the quantum search algorithm is useful when: (a) you’re doing a search where there’s little exploitable structure in the search space; but (b) you have an algorithm which lets you recognize solutions to the search problem, and so you can build the search black box.
Details of the quantum search algorithm
Now that we have an overall picture, what quantum circuits actually make the quantum search algorithm work? Rather than simply present the final algorithm, I’m going to describe a line of thinking you might imagine using to discover the quantum search algorithm. That means we’ll be making guesses, and occasionally backtracking as we realize something doesn’t work. It has the disadvantage that the presentation is longer than if I just showed you the final algorithm. But it also makes it easier to understand where the quantum search algorithm comes from, and why it works. It’s often surprisingly instructive to see reasonable ideas tried (and fail), and how it’s possible to learn from those failures.
Now, we’re looking for a truly quantum algorithm, one that exploits quantum mechanics to operate faster than a classical computer. So even though we start in a computational basis state, we should quickly move out of that state. After all, if we stayed in the computational basis we could do everything on a classical computer, and there would be no possibility of an advantage for a quantum computer.
What state might we move into?
In our circuit model, one of the gates that produces non-classical states is the Hadamard gate. Remember that the Hadamard gate takes the state to and to . A nice thing about the state is that it’s a truly quantum state which is as agnostic as it’s possible to be about the value of the bit. Suppose we applied a Hadamard gate to all the ’s at the start:
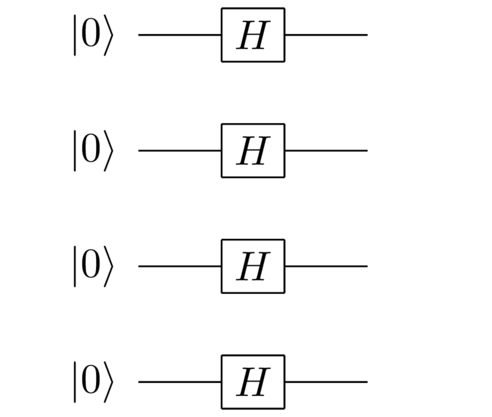
Then we’d end up with the quantum state
where we sum over both and for each qubit. Put another way, we end up with an equal superposition of all possible solutions to the search problem. It’s a starting state that’s completely agnostic about the solution. We can write this more compactly by setting to be the size of the search space, and writing the last state as an equal superposition over all possible search solutions,
This state will appear often in what follows, and it’s helpful to have some notation for it: we’ll call it , for equal superposition of possible solutions, .
Of course, this is just a guess as to how we might start out. In fact – spoiler alert! – we’ll eventually find that starting in pretty much any superposition state works. But the equal superposition is easy to prepare, and turns out to work well. It’s got the additional bonus that this state turns up in lots of quantum algorithms, so it’s good to get comfortable with it.
By the way, I said above that is the size of the search space. This isn’t always literally true. For instance, if we’re using to describe routes in the traveling salesperson problem, it might be that some bit strings don’t represent valid routes, so the actual size of the search space may be smaller than . I won’t consider that possibility in any detail, although the algorithm we’ll find is easily modified to cope with that possibility.
Now, suppose we introduce a check qubit and apply the search black box to our equal superposition state. We get the state:
That doesn’t immediately help much: if we were to do a measurement in the computational basis, we get a result where (i.e., the solution to the search problem) with probability . We’re essentially just guessing a solution.
What could we do instead if not a measurement? The most obvious thing is to apply the search black box again. Unfortunately, this adds to itself, modulo , and so we end up in the state:
This isn’t progress – we’re back where we were earlier!
Another thing to try is using a new check qubit. The simplest thing would be to apply the search black box over and over, each time with a new check qubit, so you end up with the state:
Again, this doesn’t seem all that promising. If you measured in the computational basis you’d again get a solution with probability , which is too low to be useful.
What we want is to somehow increase the amplitudes in the terms with a in the check qubit, and decrease the amplitudes when there is a in the check qubit, a way of concentrating the amplitude in the right place. Imagine, for instance, we could do the following: if the check bit is , then shrink the amplitude of the term by a factor . And if the check bit is , then double the amplitude by a factor .
Actually, that can’t work – the state would quickly become unnormalized. But maybe something like this could work, shrinking the “bad” amplitudes and growing the ”good” amplitudes, balancing things so state normalization is preserved.
Unfortunately, this isn’t possible either, at least not directly! The trouble is that quantum gates are linear. That means they don’t directly “see” the amplitudes at all. For instance, for any gate described by a unitary matrix and superposition of states,
That is, the gate doesn’t directly respond to the values of the amplitudes and at all, and so there’s no shrinking or growing of amplitudes.
Well, we haven't made much progress! Since we haven’t gotten very far with algebra, let’s instead try to visualize what we’re hoping for geometrically. We can think of ourselves as starting out in a state , and somehow trying to swing around to the solution , perhaps passing through some intermediate states along the way:
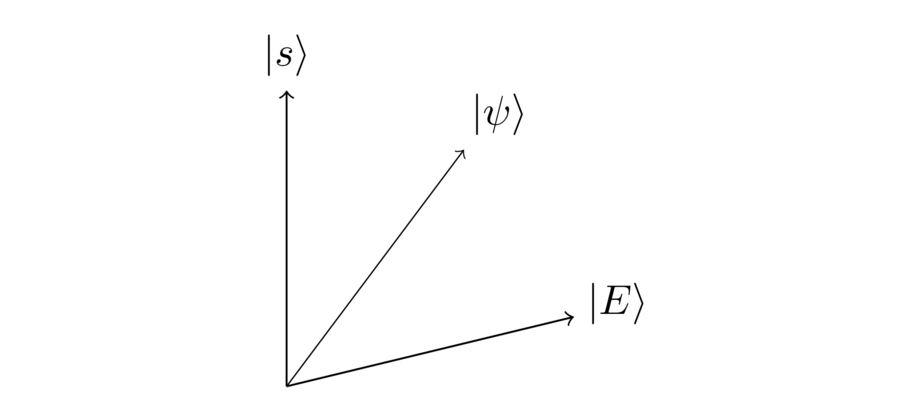
Of course, if only we knew the identity of the search solution, we could simply swing around directly. Indeed, we could solve the problem in just a single step! But we don’t know . Instead, we’re hoping to use the search black box to somehow move closer.
I want to draw your attention to one particular feature of the above diagram. I’ve shown and as being nearly orthogonal. That’s actually a pretty accurate representation of reality, since no matter what the value of , its amplitude in the equal superposition is . It’ll be useful later to have a name for the corresponding angle, so let me draw it here:
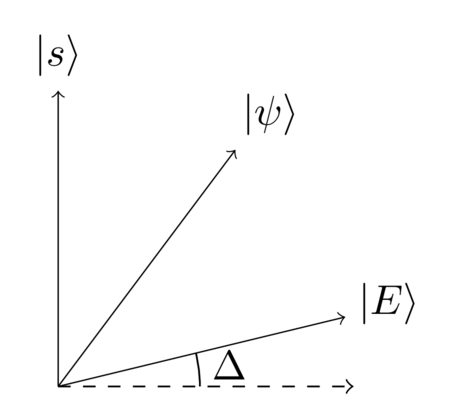
In particular, observe that the component of in the direction is just , and so .
As an aside, I’ll be expressing all angles in radians, not degrees. So a right angle is , a half rotation is , a full rotation is , and so on. I know some people prefer to think about angles in degrees, and using radians may frustrate them. On the other hand, if I worked in degrees, that’d be equally frustrating for people who prefer radians. Actually, it’d be more frustrating (and make the presentation more complex), because certain facts about trigonometry are simpler when angles are expressed in radians. An example, which I used in the last paragraph, is that for small . That becomes the much uglier if we work in degrees. So it’s better just to work in radians. End of aside.
At this point, I’m going to engage in some deus ex machina, and ask a question: what if we could somehow reflect about the solution vector ?
In fact, that turns out to be possible, and I’ll show you in a bit how to do it. For now though let’s just assume we can do it. Here’s what happens:
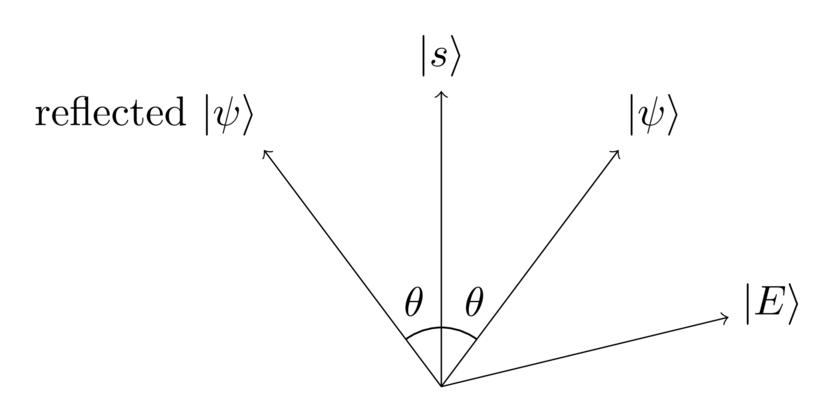
In this diagram, is the angle between and , so is the total angle between and its reflection.
You may recall from elementary plane geometry that if we do two consecutive reflections of the plane about different axes, the net result is a rotation of the plane. That seems encouraging. The obvious other vector to try reflecting about is the equal superposition . It seems plausible that if we could reflect about then we could also figure out how to reflect about . For now let’s just assume we can. The result is:
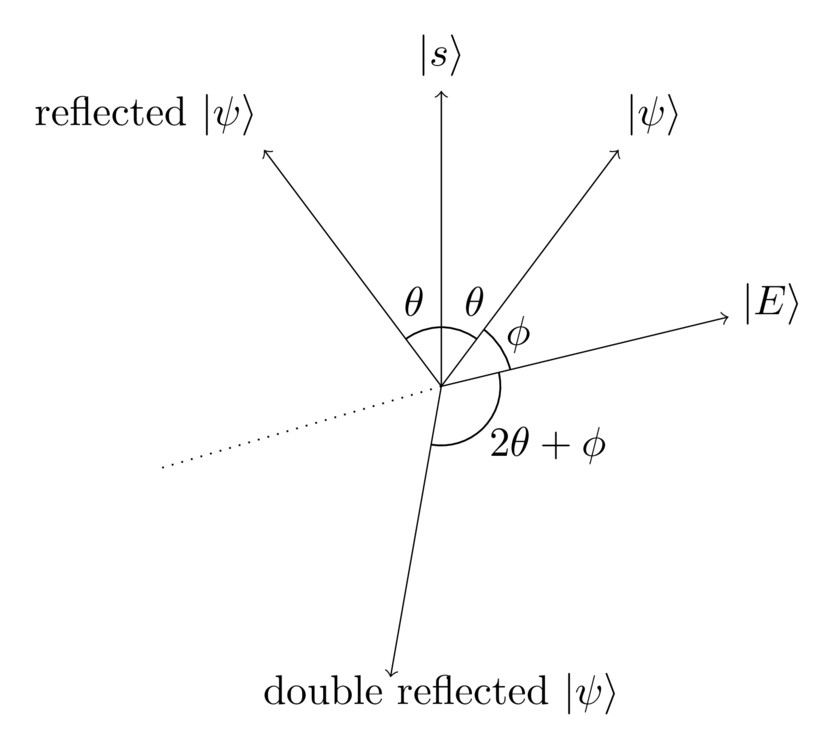
We can see from the above diagram that we’ve rotated from the original by an angle , where is the angle between the equal superposition and the vector .
Looking at the diagram, after the two reflections the quantum state is pointing in almost the opposite direction to where we started, i.e., it’s close to , but with a slight extra rotation. To see why this is true, imagine you’re in a plane, and reflect a vector about two exactly orthogonal axes – say, the usual and axes. Of course, the result is just that the vector ends up pointing in the opposite direction.
In this case, we’re not reflecting about exactly orthogonal axes, but rather about two almost-orthogonal axes. So we’d expect the net rotation to be approximately , but with a small deviation. What’s more, we’d expect that deviation to be related to the angle by which the axes failed to be orthogonal. And that’s exactly right: we have , and so a little algebra shows that the rotation is .
This rotation of is almost what we’re looking for. One thing that makes it a little hard to think about is the . In fact, a rotation by just flips a vector in the plane back and forth about the origin, effectively multiplying it by . But in the previous essay we saw that such global phase factors make no difference whatsoever to outcomes at the end of a quantum computation. So after the double reflection it's exactly as though we're working with the state shown belowIgnoring such global phase factors sometimes bother people getting into quantum computing. If it bugs you, just insert a single-qubit gate on one of the qubits.:
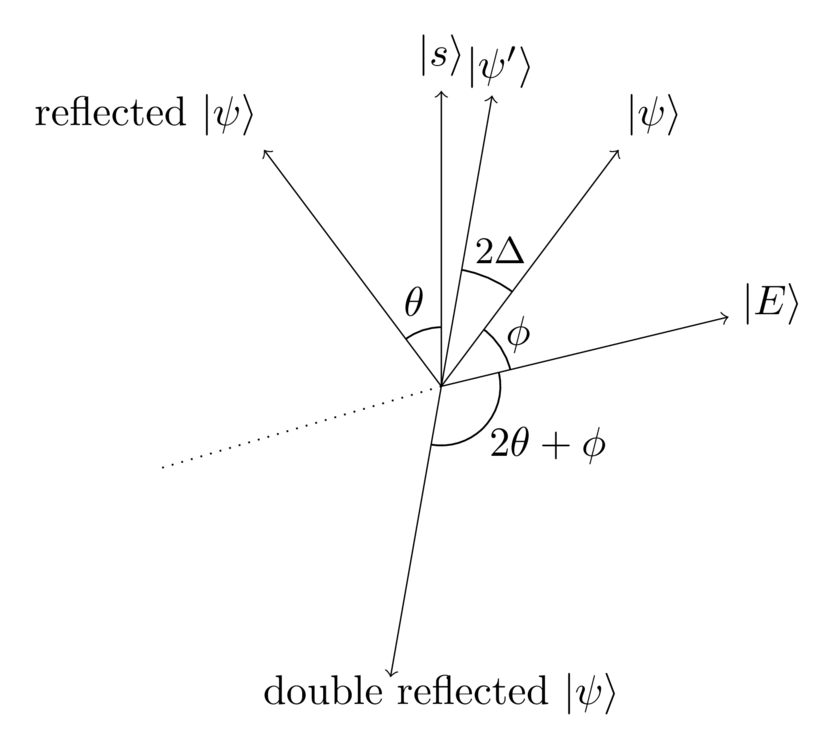
We can now see what’s going on very clearly: flipping about and then is the same as doing a rotation by (up to the global phase factor, which can be ignored). Summing up the result in one diagram, and omitting the intermediate states we have:
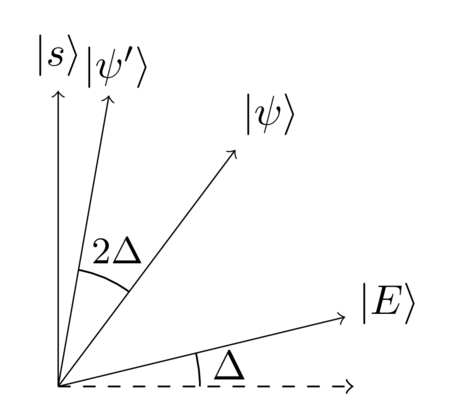
This is exciting news! It means we have a way of rotating from the starting state an angle closer to the search solution . What’s more, we can just keep repeating this operation. Maybe if we repeat it enough times we can rotate close to ?
How many times do we need to rotate to get close to ? And how close can we get?
Well, we’re rotating each time by , and ideally we’d like to rotate by a total angle of . To get as close as possible to that total angle, the number of times we should rotate is just the integer closest to the ratio of the total angle with the angle of each rotation , i.e.:
When we do so, we end up within an angle of . Remember that is small, so we’re very near the state . It should be plausible that if you measure the quantum system you’ll get the result with pretty high probability. We’ll figure out just how high that probability is shortly, but intuitively the overall picture is encouraging.
The expression above for the number of times to do the rotation has many details in it, which makes it hard to think about. The key behavior to focus on is that the number of rotations required scales with . But we saw earlier that , so scales with . The result is that if you perform roughly rotations, you’ll end up very near to the desired search solution.
(By the way, I’ve used the phrase “roughly” there because to get we used the approximation for small . In fact, a bit of fiddling around with trigonometry and algebra shows that more than rotations are never required. In practice, you’d use the exact formula with the arcsine in it. But that formula is a little complicated and somewhat opaque – the kind of thing you’d be unlikely to memorize, but would instead look up, unless for some reason you needed it often. On the other hand, is a good shorthand, capturing the essential behavior, and worth remembering, along with the caveat that the actual expression is a little more complex.)
That’s the essence of the quantum search algorithm! There are still details to be filled in, but the basic outline is as follows:
- Starting in the all- state, apply a Hadamard gate to each qubit to enter the equal superposition state .
- Repeat the following steps, known as the Grover iteration, a number of times equal to:
- Reflect about the state ;
- Reflect about the state ;
- Measure to obtain the search solution with high probability.
When you consider the remarkable feat this algorithm accomplishes – searching an -item search using examinations of that search space(!) – this is really quite simple and beautiful.
The algorithm is due to Lov Grover, who introduced it in 1996, and it’s often called Grover’s quantum search algorithm in his honor. And, as mentioned above, the two steps at the core of the algorithm are sometimes called the Grover iteration.
Before filling in the remaining details in the quantum search algorithm, let’s go through a few more spaced-repetition questions. These will help you remember many of the core elements of the algorithm. Note that a few details of the algorithm are still to be filled in, and we’ll discuss those in later sections. But we've got the core ideas now.
Exercise: At several points in this essay I ask you to ignore global phase factors. If that makes you uncomfortable, I invite you to repeat the analysis at each place I’ve made the request, not ignoring global phase factors. Show that the states output from the computation only ever change by a factor , raised to some power, and argue that measurement probabilities for the computation are not changed at all.
How to reflect about the and states?
How should we achieve the desired reflections about the and states? To answer this question, we’ll start by focusing on the state, since computational basis states are closer to our everyday way of thinking about the world. And to make it even more concrete, let’s focus on the all state, .
What would such a reflection actually do? It would mean leaving the state alone, and taking every other computational basis state to . In terms of pseudocode, if the input state is :
if x == 00...0: do nothing else: apply -1
It’s pretty easy to translate this into the quantum circuit model. You simply introduce an extra qubit that’s used as a sort of workspace for the if statement (this working qubit is often called an ancilla qubit – an unusual word in everyday speech, but easy to remember if you notice that it’s the word root for “ancillary”):
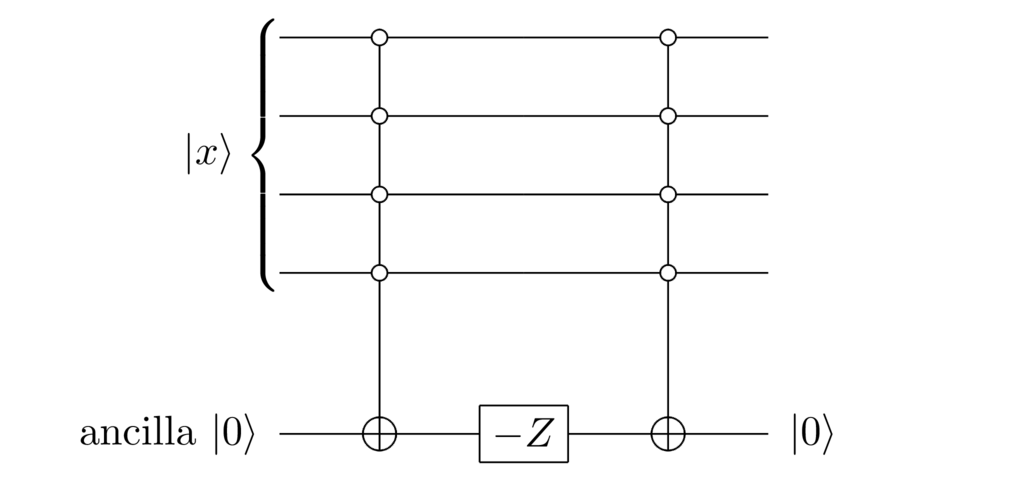
This looks different to the pseudocode, but it’s really just the quantum circuit version of the pseudocode. The first controlled gate checks to see whether is equal to , as in the if condition, flipping the ancilla qubit to if so, and otherwise leaving it as . The gate on the ancilla then does exactly what we want, doing nothing if the ancilla is set to (i.e., the if clause), and applying a factor if the ancilla is set to (the else clause). So the overall state is now when is , and otherwise.
We’re almost done. The final controlled gate is there so we can clean up the ancilla qubit, and subsequently ignore it. To do that, we apply the same controlled gate again, resetting the ancilla to , no matter what the initial computational basis state was. The result is the state when is , and when is anything else. So no matter the value of the circuit leaves the ancilla in the fixed state , and that ancilla can be ignored through subsequent computations. Ignoring the ancilla, we see that the register has been reflected about the state, just as we wanted.
There’s a rough heuristic worth noting here, which is that you can often convert if-then style thinking into quantum circuits. You introduce an ancilla qubit to store the outcome of evaluating the if condition. And then depending on the state of the ancilla, you perform the appropriate state manipulation. Finally, when possible you reverse the initial computation, resetting the ancilla to its original state so you can subsequently ignore it.
For the reflection about there’s a clever trick which can be used to simplify the circuit shown above. Instead of using an ancilla in the state, start the ancilla in the state (you do this using a NOT gate followed by a Hadamard gate on ), and then use the following circuit:
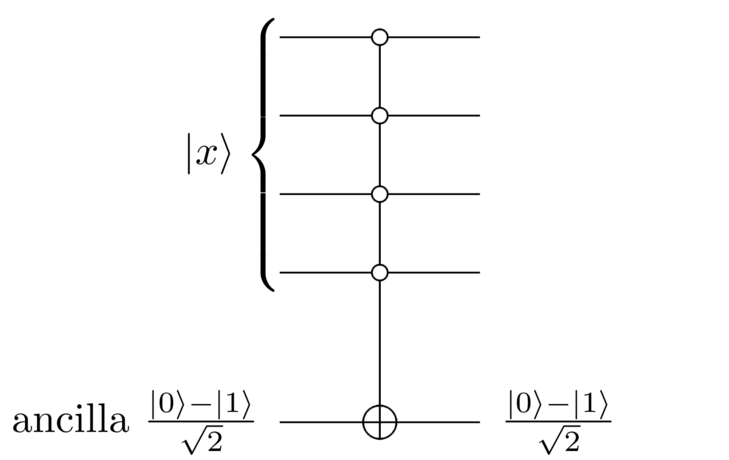
Why does this work? If , then nothing happens, and we end up in the state . If the ancilla qubit is NOTted, changing it from to , which is, of course, just . In both cases this is exactly what we wanted, except for a global phase factor of , which we can ignore. Furthermore, no matter the value of the circuit leaves the ancilla in the fixed state , and so the ancilla can be ignored through subsequent computations.
This is a nice trick, which I sometimes call the “phase trick”. I must admit, it seems a little like magic. It’s one of those things that’s easy to verify works, but it’s not so obvious how you would have discovered it in the first place. I don’t actually know the history of the trick (the earliest mention I know is in this 1997 paper), but here’s how you might have discovered it. Suppose you’d been working hard on the original circuit I showed, thinking about each element:

I don’t necessarily mean you were trying to simplify the circuit, I just mean you were messing around trying to better understand how the circuit works. And then suppose in some other context someone mentioned to you (or you noticed) that . If you’d been sufficiently deep into thinking about the original circuit, a lightbulb might go on and you’d think “Hey, the NOT gate can be used to generate a factor , without otherwise changing the state of the qubit its being applied to. That kind of factor is just what we needed in our reflections. I wonder if I can somehow use that in my original circuit?”
Having made the connection you’d eventually figure the second circuit out, though it might have required a fair bit more work before you got the circuit just right.
Reflection about the state: Having figured out how to do the reflection for the all state, it’s easy to do it for the state. We just use the search black box, in exactly the same style as the circuit just shown above:
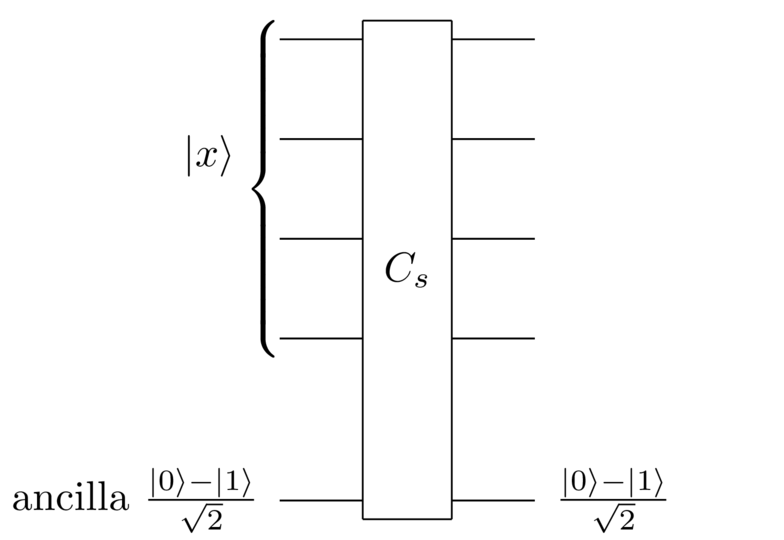
It works for exactly the same reasons as the earlier circuit: the search black box is effectively applying a NOT gate to the ancilla, conditional on being equal to . You’ll notice, by the way, that the phase trick buys us something nice here. If we’d used the original circuit, without the phase trick, we’d need two applications of the search black box to do the reflection about . So the phase trick decreases the cost of the quantum search algorithm by a factor two, a nice win.
Reflection about the equal superposition state, : The first time I thought about how to do this, I got a little paralyzed, thinking in essence: “Ooh, the state is strange and quantum, how could we possible reflect about it?”
Actually, it’s straightforward: just move the state to , reflect about , and then move the state back to . Here’s a circuit which does it:
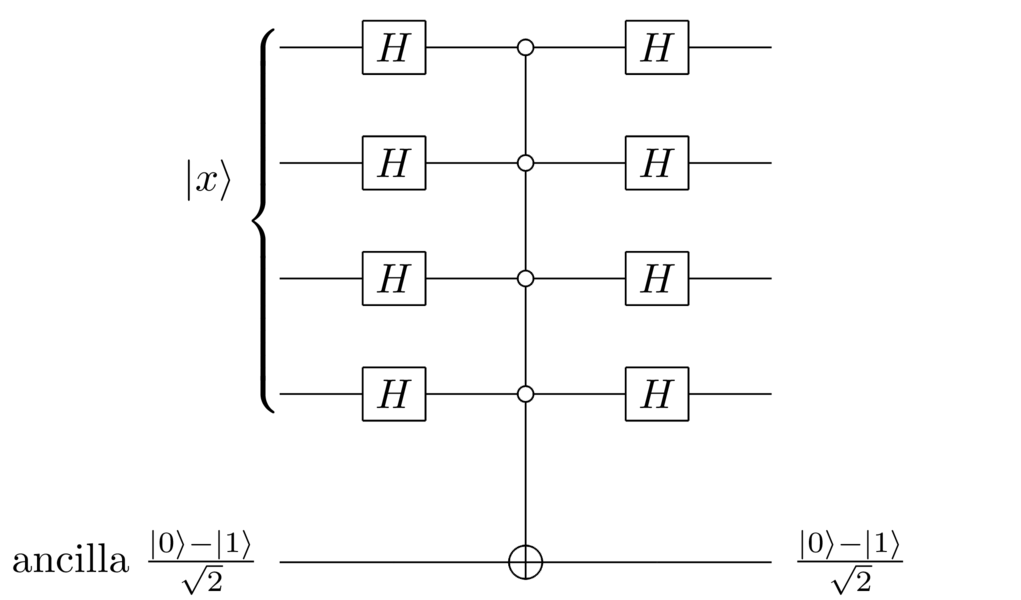
This circuit works because the product of Hadamard gates both moves to , as we saw earlier, and also moves back to , since the Hadamard gate is its own inverse.
I’m not sure what lesson to draw from my initial fear of this problem, and its actual ease of solution – perhaps that sometimes things sound scary because they’re unfamiliar, but in fact they’re simple.
Exercise: Prove that the circuit shown above does, indeed, reflect about . To do the proof, suppose the input to the circuit is , where is some state orthogonal to . Then argue that the effect of the circuit is to take this to . Up to a global phase factor this is the desired reflection.
Measuring the output
As we saw earlier, the quantum search algorithm doesn’t produce the state exactly as output. Instead it produces a quantum state which is within an angle of , as shown below (in this example has slightly over-rotated past ):
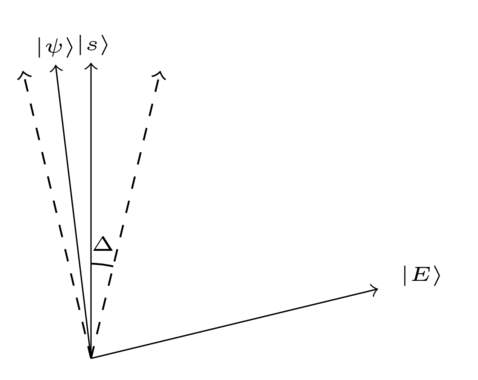
Now, the angle is small (particularly for a large search space, i.e., large , which is when we’re most interested in search), which means must be very close to . Intuitively, you’d expect a measurement in the computational basis would produce with high probability.
That intuition is correct.
In particular, the probability a computational basis measurement gives the result is just the square of the amplitude for in . That’s at least equal to , which is just .
Summing up: the probability that a computational basis state measurement gives the outcome is at least .
So, for instance, if your search space has or more elements, then the probability the search algorithm will find the correct outcome is at least , i.e., at least percent. It works even more reliably for larger search spaces.
Now, even with this high probability you might still reasonably worry about what happens if the measurement gives the wrong outcome. Fortunately, it’s possible to quickly check whether that’s happened – whatever the measurement outcome is, we can use the search black box to check whether it’s a genuine solution or not. If it’s not, we simply rerun the algorithm.
That, in turn, creates a worry that you’d need to rerun the algorithm many times. But for large – the case we usually care about when searching! – that’s extremely unlikely. A little probability calculation shows that on average the number of times needed to run the algorithm is never more than , which is very close to . Unsurprisingly, but pleasingly, our initial intuition was good: the quantum search algorithm produces the right answer, with high probability.
Summary of the quantum search algorithm
Let’s sum up our completed understanding of the quantum search algorithm:
- Starting in the all- state, apply a Hadamard gate to each qubit to enter the equal superposition state .
- Repeat the following Grover iteration a number of times equal to:
- Reflect about the state , using the circuit:

- Reflect about the state , using the circuit:

- Reflect about the state , using the circuit:
- Measure to obtain the search solution with probability at least .
- Use the search black box to check whether the measurement outcome is truly a solution to the search problem. If it is, we’re done; if not, rerun the algorithm.
That’s it, the complete quantum search algorithm!
I’ve tried to explain quantum search using what I call discovery fiction, a mostly-plausible series of steps you could imagine having taken to discover it, complete with occasional wrong turns and backtracking. Despite my attempts to make it legible, I believe there’s still something almost shocking about the quantum search algorithm. It’s incredible that you need only examine an -item search space on the order of times in order to find what you’re looking for. And, from a practical point of view, we so often use brute search algorithms that it’s exciting we can get this quadratic speedup. It seems almost like a free lunch. Of course, quantum computers still being theoretical, it’s not quite a free lunch – more like a multi-billion dollar, multi-decade lunch!
Variations on the basic quantum search algorithm: I’ve explained the quantum search algorithm in its simplest form. There are many variations on these ideas. Especially useful variations include extending the algorithm so it can cope with the case of multiple solutions, and extending the algorithm so it can be used to estimate the number of solutions if that number isn’t known in advance.
I won’t discuss these in any detail. But if you want a challenge, try attacking these problems yourself. A good starting point is to find a search algorithm for the case where there exactly search solutions, say and . You already have most of the ideas needed, but it’s still an instructive challenge to figure it out. If you’re looking for much more detail about variations on the quantum search algorithm, you can find it in Chapter 6 of my book with Ike Chuang.
What if we used a different starting state? We simply guessed that the state was a good starting state. Imagine we’d started in a different quantum state, let’s call it . And then we repeatedly reflected about and about . As before, the net result of such a double reflection is a rotation, with the angle equal to minus double the angle between and . It’s fun to think about different things one can do with such a rotation. I won’t get into it here, except to quickly mention that this observation can be used to do a type of structured search. For instance, if we know some values aren’t possible solutions to the search problem, we can actually speed the search algorithm up by making sure doesn’t appear in the initial superposition .
Can we improve the quantum search algorithm? A good question to ask is whether it’s possible to improve the quantum search algorithm? That is, is it possible to find a quantum algorithm which requires fewer applications of the search black box? Maybe, for instance, we could solve the search problem using applications of the search black box. That would be a tremendously useful improvement.
If we were truly optimistic we might even hope to solve the search problem using on the order of applications of the search black box. If that were possible, it would be revolutionary. We could use the resulting quantum algorithm to very rapidly solve problems like the traveling salesperson problem, and other NP-complete optimization problems, problems such as protein folding, satisfiability, and other famous hard problems. It would be a silver bullet, a way in which quantum computers were vastly superior to classical.
Unfortunately, it turns out that the quantum search algorithm as I’ve presented it is optimal. In particular, no search algorithm with faster than scaling is possible. This was proved in a remarkable 1997 paper. While this is a real pity, the quantum search algorithm still provides a more limited but bona fide silver bullet for speeding up a wide class of classical computations.
Exercise: Suppose that instead of performing a measurement, we instead continue performing Grover iterations. Argue that the quantum state will continue to rotate, and that we would expect the amplitude for to start to decrease.
Exercise: Argue that if we continue performing Grover iterations, as in the last question, we’d eventually expect the measurement probability for to be no more than .
What can we learn from the quantum search algorithm?
Are there any general lessons about quantum computers we can learn from the quantum search algorithm?
Although dozens or hundreds of quantum algorithms have been developed, most are for relatively specialized – indeed, often rather artificial – problems. Apart from simulating quantum systems, only a handful of inarguably extremely useful quantum algorithms are known (quantum search is one). In particular, there is as yet no good general-purpose recipe for saying when a problem can be fruitfully attacked using a quantum computer, or how. Quantum algorithm design is still bespoke.
For this reason, we should beware any too-pat explanation of why the quantum search algorithm works. If an explanation is really good, it should enable us to find interesting new algorithms, not merely provide eagle-eyed hindsight.
With that caveat in mind, I do want to make one observation. Below is an animation showing the amplitudes for all the computational basis states as the quantum search algorithm runs. In particular, it shows the amplitudes after each Grover iteration, starting at iteration and running up to the final iteration – in this case, iteration number :
You can see that the effect of the Grover iteration is to take amplitude from non-solutions and gradually concentrate it in the solution. This is just what I said earlier couldn’t be done directly. That was true, in the sense that all the gates in our circuit are still acting linearly through the amplitudes.
So what’s happening?
Well, you may remember in the last essay I asked you to guess what would happen if you applied the Hadamard gate twice in a row to the state. Intuitively, the Hadamard gate mixes the and states, so you might guess the end result would be to thoroughly mix them up.
Only that’s not what happens. Instead, here’s the two steps:
If you look closely at the final expression on the right-hand side you see that the opposite signs on the two states are canceling each other out, a phenomenon called destructive interference. Meanwhile, the two states add up, a phenomenon called constructive interference. The net result is to concentrate all the amplitude in the state, and so the outcome is just .
A similar (though more complicated) type of interference and sign cancellation is going on during the Grover iteration. Suppose we start out the iteration as follows:
We then reflect about the state, which inverts all the non- amplitudes:
The next step is to reflect about the state. The effect of this step is to achieve a cancellation similar (but more complicated) than was going on in the second stage of the double-Hadamard. In particular, this reflection reduces the amplitude a little, redistributing it over all the other computational basis states. At the same time, it takes the superposition over all the other states and reduces it slightly, redistributing it to the state. The net effect is to grow the amplitude and shrink the others, albeit “upside down”:
The global phase factor simply inverts everything, and the total effect is to grow the amplitude and shrink the others. In net, we’ve used the amplitude to cancel out some of the other amplitudes (destructive interference), and the other amplitudes to reinforce some of the amplitude (constructive interference).
This explanation is, alas, somewhat vague. I wish I could write it in a clearer way, but I can’t because I don’t really understand it in a clearer way. There’s more I could say – other perspectives, other calculations we could do. Going through all that would help, but only a little. At the core is still a clever way of using the -amplitude to cancel out non- amplitudes, and to use non- amplitudes to reinforce the -amplitude.
Quantum parallelism: One thing the quantum search algorithm has in common with many other quantum algorithms is the use of large superposition states. For instance, the equal superposition state shows up in many quantum algorithms. It’s a pretty common pattern in those algorithms to then modify that state so each term picks up some information relevant to the solution of the overall problem, and then to trying to arrange cancellation of terms. This pattern is often known as quantum parallelism.
Upon first acquaintance, this seems much like a conventional classical computer running a randomized (i.e., Monte Carlo) algorithm. In particular, it’s a bit like trying a random solution, and then computing some information relevant to the overall problem you’re trying to solve. But what is very different is that in a classical computer there’s no way of getting cancellation between different possible solutions. The ability to get that kind of interference is crucial to quantum computing.
Why we use clean computation: Earlier, I promised you an explanation of why we used clean computation. In fact, for the interference to work, it’s essential that no other qubits are changed by the computation. Suppose we had a sum involving working qubits in lots of different states, something like (omitting factors) , i.e., a non-clean computation. We couldn’t get any sort of cancellation (or reinforcement) between terms with different values of . Those other qubits would be storing information which prevented cancellation of terms. That’s why clean computation is helpful.
This helps explain why clean computation is useful, but may leave you wondering how you could ever have invented clean computation in the first place?
In fact, historically the uncomputation trick for clean computation was discovered for reasons having nothing to do with quantum algorithms or with interference. It was discovered by people who were trying to figure out how to make conventional classical computers more energy efficient. Those people had come up with an argument (which I won’t describe here) that working bits actually contributed to energy inefficiency. And so they discovered uncomputation as a way of minimizing that energy cost. It was only later that it was realized that clean computation was extremely useful in quantum computing, especially for getting interference effects.
This is a pattern which often occurs in creative work far beyond physics: ideas which arise in one context are often later reused for completely different reasons in another context. I believe that if that prior work on energy-efficient computing hadn’t been done, it might have taken quite a bit more effort to come up with the quantum search algorithm.
Concluding thoughts: You’ve now worked through the details of a powerful, widely-usable quantum algorithm. Other algorithms are known, some of which – notably, the quantum algorithm for factoring integers – offer even larger speedups over known classical algorithms. Still, if and when quantum computers are eventually built the quantum search algorithm is likely to be an extremely useful application. What’s more, many of the ideas used in the search algorithm are used in other quantum algorithms.
Thanks for reading this far. In the coming weeks, you’ll receive a notification containing a link to your first review session. In that review session you’ll be retested on the material you’ve learned, helping you further commit it to memory. It should only take a few minutes. In subsequent weeks you’ll receive more notifications linking you to re-review, gradually working toward genuine long-term memory of all the core material in the essay.
Thanks for reading this far. If you’d like to remember the core ideas of this essay durably, please set up an account below. We’ll track your review schedule and send you occasional reminders containing links that will take you to the review experience.